linercow.blogg.se - Surface area of rectangular prism

#Surface area of rectangular prism how to#

This gives us our simplified formula as A = bh + 3bL. 2.) We can use this to replace (s1 + s2 + s3) in the formula with 3b. Problem 2: If we are given a triangular prism that has a base formed by an equilateral triangle, how can we simplify the surface area formula before solving it? Solution: 1.) Since an equilateral triangle is made of three equivalent side lengths, we know that our s1 = s2 = s3. A = 123.31 4.) The surface area of the right-angled triangular prism is 123.31. Use one color for the top and bottom, another color for the front and back, and a third color for the right and left sides.

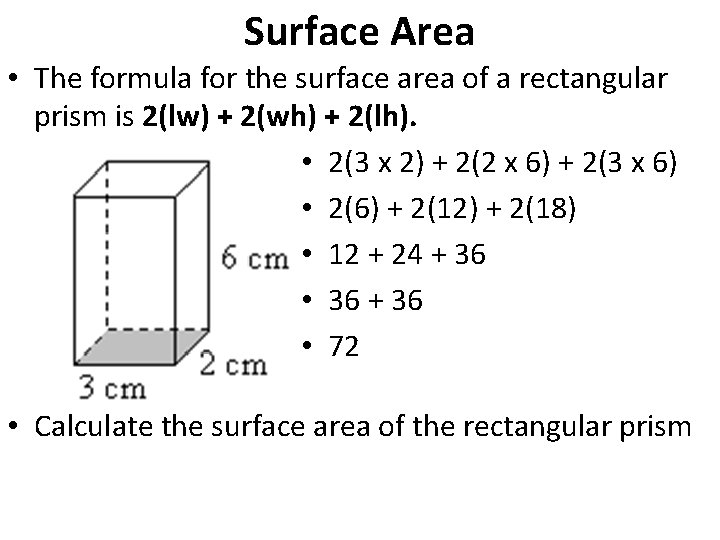
Prior to the lesson, cover one large gift box with paper. 3.) Now let’s plug our known values into the surface area formula. area, length, width, height, surface area, rectangular prism (earlier grades) Student/Teacher Actions (what students and teachers should be doing to facilitate learning) 1. The following diagram shows the formula for the surface area of a rectangular prism. When you have a cube, finding the area of one face allows you to find the total.

#Surface area of rectangular prism how to#

Using the Pythagorean theorem, we get: (s3) 2 = 4 2 + 7 2 s3 = 8.062. Examples, videos, worksheets, stories, and solutions to help Grade 6 students learn how to find the surface area of a prism. The surface area of a rectangular prism is the total area of all six faces. The volume of a rectangular prism is the length times the width times the height.

Welcome to the Surface Areas section at.

2.) We are still missing s3, which is the hypotenuse of the right triangle.

To find the surface area of this triangular prism, find the area of the three rectangles and two triangles in its net and add all the areas together. Solution: Given, base area 60 square units, base perimeter 40 units and length of prism 7 units Thus, the surface area of the right triangular prism, Surface Area (Perimeter of the base × Length of the prism ) + (2 × Base Area ) SA (40 × 7) + (2 × 60) SA (280 + 120) SA 400 square units.

A 4 x 8 x 2 rectangular prism has a surface area of 112 square units from these calculations. These will also be our first two sides, so s1 = 4 and s2 = 7. I believe that there might be a misunderstanding. Solution: 1.) Since the base of the prism is formed by a right triangle and we know the leg lengths of the triangle, we can use the legs as the base and height. Find the surface area of the triangular prism. The lateral faces of the prism are formed by a rectangle with a length of 5.

Problem 1: The bases of a triangular prism are formed by a right triangle with leg lengths of 4 and 7.